Blog de los números racionales: https://goo.gl/kv9D2R
Vídeos de números racionales en YouTube :
Suscríbete a matemática QuidiMat - Guillermo: https://goo.gl/Kc6vkQ
1) LOS NÚMEROS RACIONALES EN LA RECTA NUMÉRICA, COMPARACIÓN, ORDEN Y DENSIDAD:
La recta numérica racional está conformada por un conjunto de puntos colineales (puntos que se encuentran en una misma recta), desde el menos (- ¥ ) infinito hasta el más infinito (+ ¥ ).
A cada número racional le corresponde un punto en la recta numérica racional, recíprocamente, a punto de la recta numérica racional le corresponde un número racional.
El conjunto de números racionales es denso, porque, entre dos números racionales existe otro número real.
Ejemplo:
La estatura (talla) de una alumna es 1,47 metros, ubica en la recta numérica racional.
Solución:
Construimos la recta numérica para los números racionales
La estatura de la alumna 1,47 metros está comprendido entre los valores de 1 y 2
Simbólicamente: 1 < 1,47 < 2
Ampliamos la recta numérica comprendida entre los intervalos 1 y 2, al décimo, es decir, dividimos en diez partes.
La estatura de la alumna 1,47 metros está comprendido entre los valores de 1,4 y 1,5
Simbólicamente: 1,4 < 1,47 < 1,5
Ampliamos la recta numérica comprendida entre los intervalos 1,4 y 1,5, al centésimo, es decir dividimos en diez partes.
Ubicamos la estatura de la alumna 1,47 en la recta numérica
En la recta numérica racional la estatura de la alumna 1,47 está ubicado en:
B) COMPARACIÓN DE NÚMEROS RACIONALES
LEY DE TRICOTOMIA
Dados dos números racionales a y b se cumple solamente una de las siguientes afirmaciones:
a < b ; a > b ; a = b
Si dos números se encuentran ubicados en la recta numérica, es mayor el número que se encuentra a la derecha y es menor el número que se encuentra a la izquierda.
C) ORDEN DE LOS NÚMEROS RACIONALES
Al ordenar números racionales en forma ascendente o creciente se realiza del menor al mayor número
Al ordenar números racionales en forma descendente o decreciente se realiza del mayor al menor número
ACTIVIDAD DE APRENDIZAJE
SITUACIÒN PROBLEMÀTICA
Muchas alumnas no saben con precisión su edad, es decir, cuando se les pregunta sobre su edad, responden solo en años, esto no es correcto, falta precisar en términos de números racionales. Esto hace que al comparar las edades de dos alumnas se tenga dificultad en establecer quien es mayor o quien es menor, consecuentemente no se puede ordenar por edad, el problema es mayor al no poder explicar matemáticamente esta diferencia más aún no se pueda expresar en el lenguaje simbólico matemático.
1) Completa la tabla Nro. 01 con las edades de las integrantes de tu equipo en años, meses y expresión decimal. Fecha de nacimiento y edad actual. El equipo debe estar conformado por 4 estudiantes
TABLA Nro. 01
EDAD DE ALUMNAS EN AÑOS, MESES Y EXPRESIÒN DECIMAL
N°
|
APELLIDOS Y NOMBRES
|
FECHA DE NACIMIENTO
|
EDAD ACTUAL
|
EDAD ACTUAL EN
EXPRESIÓN DECIMAL
(Al centésimo)
| ||||
DÍA
|
MES
|
AÑO
|
AÑOS
|
MESES
|
DÍAS
| |||
1
| ||||||||
2
| ||||||||
3
| ||||||||
4
| ||||||||
NOTA: Escribe la fecha en que se rellena la tabla
2) Ubica en la recta numérica las edades de las integrantes de tu equipo con aproximación al centésimo.
3) Ordena a las integrantes de tu equipo por edad.
A. ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HOMOGENEAS
Dos o más fracciones son homogéneas si tienen el mismo denominador. Para resolver se escribe el mismo denominador y se suman o restan los numeradores.
B. ADICIÓN DE FRACCIONES HETEROGENEAS
Convirtiendo a fracciones homogéneas:
Ejemplo:
Calculando el mínimo común múltiplo:
Ejemplo:
Aplicando el teorema:
C. SUSTRACCIÓN DE FRACCIONES HETEROGENEAS
Convirtiendo a fracciones homogéneas:
Ejemplo:
Calculando el mínimo común múltiplo:
Ejemplo:
Aplicando el teorema:
ACTIVIDAD DE APRENDIZAJE
1) Resuelve aplicando los tres métodos:
2) Un rectángulo tiene 8,5 cm de largo y 7,2 cm de ancho. Construye con hojas de colores y calcula la medida del perímetro.
3) Uno de los lados de un rectángulo mide la mitad del otro. Si el perímetro mide 31 cm. Calcula la medida de cada lado y construye utilizando hojas de colores.
4) María Elena compró 1 kilogramo de helado, pero en su casa ya había un cuarto de kilogramo. Si en total comieron medio kilogramo. ¿Cuántos kilogramos de helado queda?
5) Formula un problema de adición y sustracción de números racionales y resuelve.
TEOREMA: MULTIPLICACIÓN DE FRACCIONES
Al multiplicar fracciones:
El numerador del resultado o producto se obtiene multiplicando los numeradores del multiplicando y multiplicador.
El denominador del resultado o producto se obtiene multiplicando los denominadores del multiplicando y multiplicador.
Ejemplos:
TEOREMA: DIVISIÓN DE FRACCIONES
Al dividir fracciones:
Se multiplica en aspa el numerador del dividendo por el denominador del divisor, este resultado es el numerador del cociente o resultado.
Se multiplica en aspa el denominador del dividendo por el numerador del divisor, este resultado es el denominador del cociente o resultado.
Ejemplos:
ACTIVIDAD DE APRENDIZAJE
1) Resuelve:
2) Para construir un edificio se cuenta con un presupuesto de S/. 1 200 000 para tres gastos: la construcción, los acabados y los gastos administrativos. Se ha estimado que para la construcción de cada piso se debe invertir aproximadamente S/. 111 650,50. Si para gastos administrativos se ha destinado S/. 24 000. ¿Cuánto dinero queda para los acabados?
3) La profesora Xiomara tiene S/. 72 y gasta 2 / 7 en comprar lapiceros y 3 / 8 en la compra de cuadernos. ¿Cuánto de dinero le queda?
4) Una bodega tiene 220 tarros de leche y vende cada tarro de leche a S/. 2,90. Durante la mañana vende los 2 / 5 del total y por la tarde, 3 / 4 del resto. ¿Cuántos tarros de leche no se vendieron y cuánto dinero se obtuvo en la venta?
4) POTENCIACIÓN DE NÚMEROS RACIONALES
La potenciación es una operación matemática, entre una base y un exponente, donde el exponente nos indica el número de veces que debe multiplicarse la base, para obtener un resultado llamado potencia.
En nuestro ejemplo se lee: "dos tercios elevado al exponente 3" o "dos tercios al cubo".
En nuestro ejemplo se lee: "dos tercios elevado al exponente 3" o "dos tercios al cubo".
LAS PARTES O ELEMENTOS DE LA POTENCIACIÓN:
TEOREMAS
a y b Î Q se cumplen los siguientes teoremas o propiedades:
1) EXPONENTE UNO
Un número racional elevado al exponente 1 es igual al mismo número
2) EXPONENTE CERO
Cualquier número racional elevado al exponente 0 (cero) es igual a 1 (uno).
3) PRODUCTO DE POTENCIAS DE BASES IGUALES
La multiplicación de dos potencias de igual base es igual a la misma base y se suman los exponentes.
4) COCIENTE DE POTENCIAS DE BASES IGUALES
La división de dos potencias de igual base es igual a la misma base y se restan los exponentes del numerador y denominador.
5) POTENCIA DE UNA MULTIPLICACIÓN
La multiplicación de números racionales elevado a un exponente es igual a cada factor elevado al exponente, es decir, el exponente se distribuye como exponente de ambos factores.
6) POTENCIA DE UNA DIVISIÓN
En una fracción elevada a un exponente, este último se distribuye como exponente del numerador y denominador.
7) POTENCIA DE POTENCIA
En una potencia de potencia se escribe el número y se multiplican los exponentes.
8) POTENCIA DE EXPONENTE NEGATIVO
Un número racional elevado a un exponente negativo se intercambian numerador con denominador y el exponente cambia de signo.
ACTIVIDAD DE APRENDIZAJE
Resuelve:
5) RADICACIÓN DE NÚMEROS RACIONALES
La radicación es una operación contraria a la potenciación, consiste en buscar un número que multiplicado tantas veces como indica el índice de la raíz nos de la cantidad sub radical o radicando.
En nuestro ejemplo se lee: “la raíz cúbica de menos ocho veintisieteavos es igual a menos dos tercios”.
TEOREMAS
" a, b, c y d Î Q se cumplen los siguientes axiomas o propiedades:
1) CUANDO EL RADICANDO ES POSITIVO:
Si la cantidad subradical o radicando es positivo, se puede extraer raíz de índice par e impar.
Ejemplo:
2) CUANDO EL RADICANDO ES NEGATIVO:
Si la cantidad subradical o radicando es negativo, sólo se puede extraer raíz de índice impar.
Ejemplo:
Ejemplo:
3) RAÍZ DE UN PRODUCTO:
4) RAÍZ DE UN COCIENTE:
5) RAÍZ DE UNA POTENCIA:
6) DE EXPONENTE DEL RADICANDO A EXPONENTE DE LA RAÍZ:
7) RAÍZ DE UNA RAÍZ:
8) ÍNDICE DE LA RAÍZ Y EXPONENTE DEL RADICANDO TIENEN EL MISMO VALOR:
9) COMO INGRESAR UN NÚMERO AL RADICAL:
10) CAMBIAR EL ÍNDICE DE UNA RAÍZ:
ACTIVIDAD DE APRENDIZAJE
Resuelve:
Vídeos de números racionales:
Los números racionales en la recta numérica:
Los números racionales en la recta numérica, fracciones, decimales: https://youtu.be/Geq5TlPXbGs
Los decimales y fracciones en la recta numérica: https://youtu.be/t11Td8HQmLo
Adición y sustracción de números racionales: https://youtu.be/JdjME7QUBzA
Suma y resta de fracciones con diferente denominador: https://youtu.be/f94cP06mTDA
Multiplicación y división de números racionales: https://youtu.be/HmF9YBHpd30
Multiplicación y división de fracciones heterogéneas: https://youtu.be/F9kxP9uSRWkMultiplicación y división de números racionales: https://youtu.be/HmF9YBHpd30
Potenciación de números racionales: https://youtu.be/yvFlXGzYhyo
Radicación de números racionales, fracciones: https://youtu.be/j7HJBJKgf-A
Problemas de números racionales por el método de Polya: https://youtu.be/P50Py3L8x8o
Problemas de sustracción de números racionales - George Polya: https://youtu.be/EqwXNUZJhWc
Números racionales - Indice de masa corporal y estado nutricional de estudiantes:
Método de Polya en operaciones con fracciones: https://youtu.be/01W-wjubXk0
Problemas de sustraccion de fracciones, método de Polya: https://youtu.be/Zzh7UL-wPck

























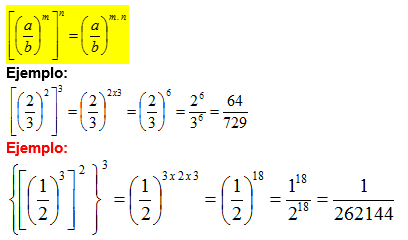

















No hay comentarios:
Publicar un comentario